OPRR Flash Depth Activities

Search Extension

Explore DeFi lending: Components, formulas, and use cases

23-04-23 12:29

Read this article in 30 Minutes

AI summary

View the summary

DeFi Lending Concepts Part 1: Lending and Borrowing

Original article by Tal

Kxp, Blockbeats

This article, the first in a three-part series, discusses how DeFi lending protocols work - their key components, formulas, and use cases. Along the way, we'll emphasize that although protocols use different and creative naming methods, they tend to repeat, iterate, and share core concepts. One of these blog posts details how to use ERC20 Token to represent a user's share of the lending pool. We'll start by analyzing the unique elements of these protocols and provide technical concepts to distinguish how they work.

Lending pool

In traditional finance (or TradFi), lending is adjusted by a third party financial institution. These financial institutions are entrusted with two key tasks: to compel lenders to pay interest to lenders, and to assess and prevent parties deemed to be discredited from participating in these activities.

In contrast, in decentralized finance (or DeFi), third-party borrowers and lenders are not to be trusted. This lack of trust has inspired an innovative design to facilitate the lending process along the chain.

A lending pool is a smart contract. DeFi users can deposit assets (typically ERC20 tokens) with the intention of using the contract to lend out their deposited assets. Other users can interact with the lending pool and take advantage of instant loans, borrowing against assets in the pool.

Compared with traditional financial methods, lending pools have some significant advantages in terms of lending, such as:

, & have spentIn DeFi, loans are not subject to the 1:1 availability of the loan funds to the borrowed amount. Instead, funds from all users of the protocol are deposited into the pool, creating an inventory of tokens large enough to meet loan demand immediately.

, & have spentDeFi does not need a repayment plan. Loans are executed against previously deposited collateral, and users can choose to repay at any time.

At this point, you may be thinking, "Why borrow assets on a loan agreement if I have to put up assets of equal (or even overvalued) value as collateral? Shouldn't I sell the collateral and buy the borrowed assets?"

Indeed, this DeFi lending agreement appears to allow only fully collateralized (or over-collateralized) loans, opening the door to an interesting "trading" method: leverage.

Let's say you're pretty bullish on WBTC and pretty sure its value will skyrocket! You can deposit some WBTCS (worth $1000) on your favorite lending agreement, then use it to borrow some stablecoins (e.g. USDC), and then use those stablecoins to buy more WBTCS on an exchange (for our scenario, assume half of your initial deposit, i.e. $500). In this case, the value of your exposure to WBTC is $1,500, and your initial deposit is only $1,000.

But what if you put your $500 WBTC collateral into the agreement to borrow more USDC? This process is called excess leverage, and you can keep doing it until you exceed your ability to borrow, and the policies of the agreement prevent you from doing so.

In a similar situation, suppose you're pessimistic about WBTC (it's Crypto winter, after all). You can do the opposite of what we did in our previous scenario and borrow WBTC by depositing USDC as collateral into the protocol and then immediately replacing it with more stablecoins. If your prediction comes true and the price of WBTC drops, you can open (and close) a short position in WBTC by buying the same amount of WBTC at a cheaper price on the exchange, paying off the loan and gaining excess USDC.

Share Token

As with traditional finance, users who deposit their assets in a lending pool are incentized to keep the money for a long time and earn interest on the deposits. Interest accrues over time as a percentage of the subscriber's deposit in the Agreement and is claimed by its corresponding depository subscriber. The longer users keep assets in the pool, the more interest they earn.

How does the protocol record each user's share in the pool? When one user deposits assets into the pool, their "share" dilutes the share of all users, and the protocol reflects this accordingly. However, the protocol does not directly track and update each user's pool share, but instead only handles changes in depositors' shares without actively updating other users' shares each time they are withdrawn or deposited.

You might think this agreement allows you to have your cake and eat it. But that's not really the case:

The agreement handles interest issuance by minting and destroying ERC20 tokens, which we call "share tokens," which represent a lender's share (or percentage of deposit assets) in the loan pool. This "share Token" design automatically adjusts the dilution of other "shareholders" shares to reflect the minting and destruction of "shares" in proportion to the deposits or withdrawals of their underlying assets.

Below, we provide practical examples of how different protocols use "share tokens" and discuss their similarities.

aToken: AAVE's "Share Token"

aToken is AAVE's revenue-generating Token, minted and destroyed by the loan pool when the assets are deposited and withdrawn.

aToken is an ERC20-like Token that is integrated into the AAVE protocol, so that each of the different markets that a user can enter (deposit collateral) has a corresponding aToken.

If we look at the AAVE loan pool contract, we can see the basic action that occurs when a user deposits assets into the pool:

We can see that aToken corresponding to the user-deposited market will be called the "cast" function.

We can see that the actual quantity to be cast is:

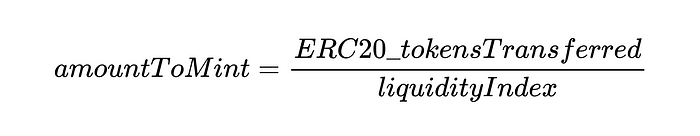
As shown in the figure above, in this example, the user joins a market that has already earned some interest on previous deposits. The equation above helps us understand this because it shows how interest accruals for all users can be taken into account using a global index that is updated at various operations (deposits, withdrawals, and so on).

When users withdraw their underlying assets, the liquidityIndex is used as a multiplier to calculate the number of tokens owed in the transaction.

Here's the relevant code snippet from the loan pool contract:

Here, the balanceOf the aToken contract is a little odd. After all, we have just determined that the number of aToken minted is different from the number of underlying assets deposited. How does calling IAToken(aToken).balanceOf(address(user)) produce the number of underlying assets that the user is about to extract (as shown at the bottom of the function)? Here's why:

, & have spentWhen users withdraw their assets, their aToken will be destroyed. These destroyed Atokens keep the total number of Atokens owned by other users in proportion to their shares, which are taken after the user assets have been drawn.

, & have spentThe market rate at which users withdraw funds is updated with each withdrawal.

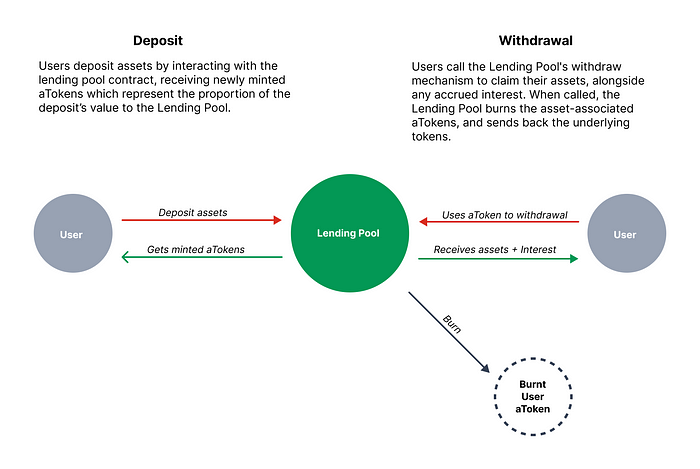
As we stated earlier, aToken is aToken similar to ERC20. We emphasize that they are "similar" to ERC20 tokens because of the unique properties of their balanceOf functions. In regular ERC20 tokens, the balanceOf function returns the number of tokens owned by an address.

Since aToken represents the share of the pool, rather than the direct value, the balanceOf function aToken returns the number of underlying tokens owed by the protocol to the user to compensate for its deposit.

Here, the balanceOf function overrides the balanceOf function in the inherited aToken contract. As a result, the balanceOf logic in the example logic is performed instead of the regular (inherited) mapping lookup for the number of user tokens.

The above mentioned Token and then multiplied by the number getReserveNormalizedIncome results, the function performs the following logic:

We can identify the branch here:

, & have spentIf the reserved data has been updated in the block: returns the liquidityIndex value for the market as it has been updated.

, & have spentOtherwise: We need to see what's happening in the calculateLinearInterest to figure out the next flow.

currentLiquidityRate and lastUpdateTimestamp from the ReserveData object of the current market are passed into this function. The result of this function is:

Let's break down the components of this equation to better understand the gist of the linearInterest value:

, & have spentcurrentLiquidityRate: Think of this as the annual interest rate (APY) for our market

, & have spentblock_{timestamp} - lastUpdatedTimestamp: The amount of time that has elapsed since the last update

Note: Since we selected the second branch in getNormalizedIncome, this value is guaranteed to be positive at this point.

Therefore, we can view this interest accrual mechanism as a simple interest compounding mechanism that compounds in each block. Now that we have determined the amount of interest to accumulate for the user, we simply multiply that value by the liquidity index and then do the user's normalized income multiplication in the balanceOf function:

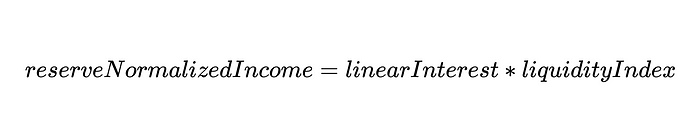
Now that we understand the logic behind aToken, we still need to solve the mystery of how liquidityIndex works.

In the following example, liquidityIndex can be defined as the interest accrued on reserves over a period of time:

Review the liquidityRate variable mentioned earlier - we will now discuss its use in calculating liquidityIndex. Interest accrues only if the liquidityRate is greater than 0 - in other words, interest accrues only if there is any APY in that market. It makes sense.

Let's quickly review calculateLinearInterest in action:

The above logic can be translated into the following equation:

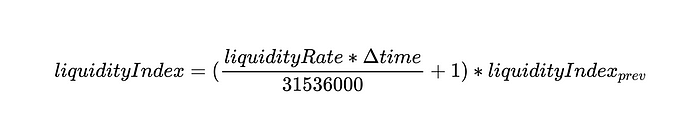
As we can in DefaultReserveInterestRateStrategy. See sol contract, liquidityRate is defined by the following way:

Therefore, it can be written as:

The overall borrowing rate (overall borrowrate) is defined here as:

We can write this as:

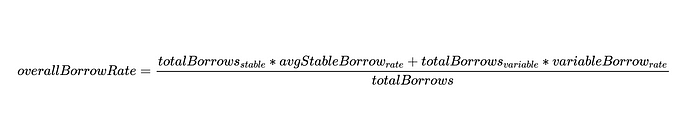
utilizationRate can be defined as: Utilizationrate

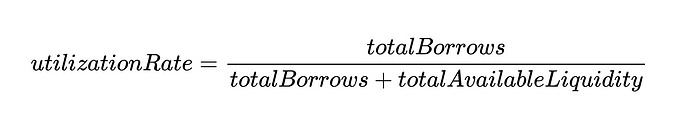
In defining utilization, it is easier to consider the ratio between liquidity in reserves (liquidity currently lent) and total liquidity in the market, which can be simplified as:

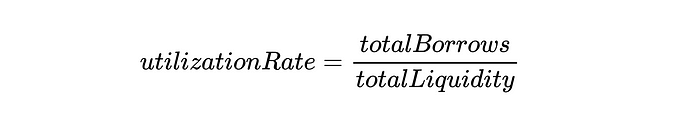
Now we can use these two definitions to write the equation for the liquidity index:

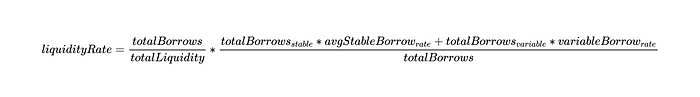
Since totalBorrows exists in both numerator and denominator, we can write it as:

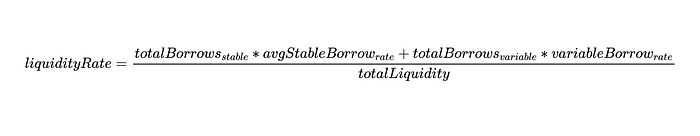
Enough about the equation for the liquidity index for now, and we'll come back to that definition later.

cToken: Compound "Share Token"

Let's move on to our next example of a loan agreement, Compound.

Compound uses "share tokens" called Ctokens to handle borrowing and lending. This Token accounts for all assets in the Compound protocol that can be used for user loans.

Similar to what we discussed in AAVE V2, Compound "share tokens" are minted and used to redeem the underlying assets.

The exchange rate used by the Compound is similar to the AAVE V2 liquidity index to determine how many Ctokens should be minted. The exchange rate is a function of:

Let me explain the key terms here:

,totalCash: The number of ERC20 base tokens owned by the cToken account.

, & have spenttotalBorrows: The amount of ERC20 base tokens that borrowers lend out on the market.

, & have spenttotalReserves: A limited amount of ERC20 base tokens retained which can be withdrawn or transferred by governance.

, & have spenttotalSupply: The ERC20 function that returns the total supply of Ctokens.

With this background, we can write the Compound exchange rate equation:

When users deposit ERC20 tokens, the exchange rate determines how many Ctokens will be minted in return:

The number of Ctokens to be minted is defined by the following equation:

eToken: Share Token of Euler

To further consolidate the similarities between these protocols, let's analyze Euler, another lending protocol, to see how it handles borrowing.

In the following example, the deposit function allows the user to deposit an ERC20 Token in exchange for an eToken.

As we have seen, internalAmount is the number of Etokens minted for this transfer.

Again, the Compound name and function exchangeRate directly overlap.

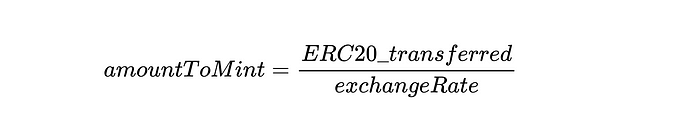
Let me explain the key parameters used to calculate exchange rates:

, & have spentpoolSize: The result of calling the balanceOf (address) function at the pool contract address in the underlying asset's ERC20 contract.

, & have spenttotalBorrows: The total amount of underlying ERC20 tokens lent, which is not currently in the pool.

, & have spenttotalBalances: total balances of all eToken holders.

So the equation would be:

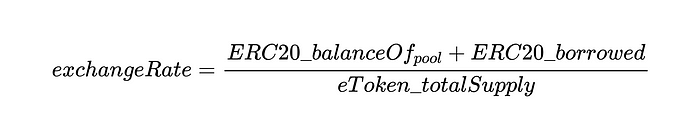
summarize

We have covered 3 loan agreements:

, & have spentAAVE V2

, & have spentCompound

, & have spentEuler

We have examined how "share tokens" are minted and how they are exchanged for deposit assets through pools of borrowing and lending.

The three equations we proposed can be reduced to a simple equation:

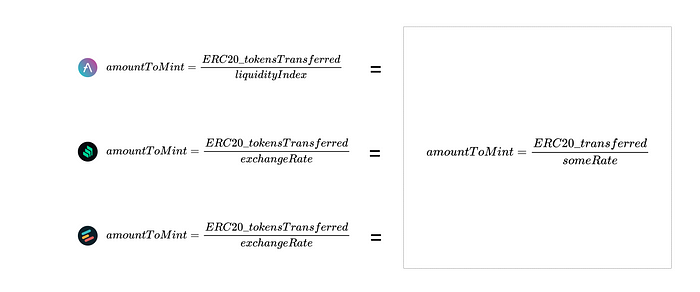
Keep in mind that exchange rates can be defined in any way defined by the agreement. These arbitrary exchange rates can increase the number of tokens minted (if less than 1) and decrease the number if more than 1.

We've already seen some similarities between the someRate variable in AAVE V2 and Compound. In Compound, someRate is:

For AAVE V2, someRate is defined as follows:

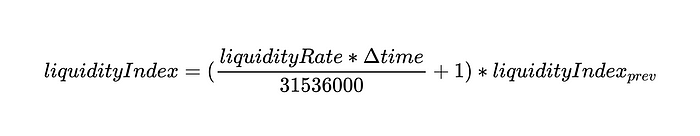
The liquidity index is defined as:

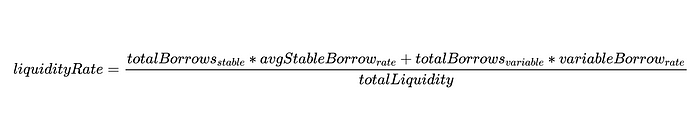
Although we cannot generalize the exchange rate of each protocol into a formula, for AAVE2 and Compound, we know that the exchange rate is a function of the total liquidity in the market. Returning to our equation, given that totalLiquidity is the total amount of basic tokens of ERC20 in the market, the numerator of exchangeRate expression and the numerator of liquidityRate are functionally the same.

In short: these agreements are essentially similar. While they may sometimes use different terminology, when they are broken down into equations, each component serves a similar purpose in its implementation. We invite readers to choose a loan agreement at random and check whether the generalizations we discuss here apply to that agreement as well. Please feel free to let us know if applicable.