V 神科普的「Danksharding」到底是什么？

原文标题：《情人节，V 神科普的「Danksharding」到底是什么？》

原文来源：DeFi 之道

北京时间 2 月 14 日情人节当晚，以太坊创始人 Vitalik Buterin 联合以太坊基金会（EF）研究人员 Dankrad Feist 一起举办了一场关于扩容解决方案「Danksharding」的教育研讨会，如果你想了解区块链如何在增加「去中心化」和「安全性」属性的同时大规模实现扩容，那么这场研讨会就是一个好的切入点。

注：关于「Danksharding」对以太坊的意义，建议读者先阅读一下《一文了解以太坊的「扩容杀手锏」danksharding》这篇文章。

以下内容来自 Dankrad Feist 提供的《Dude, what's the Danksharding situation‌?》PPT，如果你想观看完整的研讨会视频，可以访问以太坊基金会的官方 youtube 频道‌。

概述

1、什么是旧的：

（1）数据分片；

（2）使用 KZG 承诺的数据可用性；

（3）使用分离分片方案进行原始数据分片；

2、什么是新的：

（1）提议者-构建者（数据生成者）分离 (PBS)；

（2）crList；

（3）2D 方案；

（4）建议的架构

3、总结优点和缺点

一、什么是旧的

1.1 数据分片

1、为 Rollup 和其他扩容解决方案提供数据可用性（DA）；

2、数据的含义由应用层定义；

（1）以太坊基础共识（全节点和验证者）除了确保数据可用外不承担任何责任；

（2）为什么没有执行分片？与原生执行相比，rollup 二层网络的效率要高 100 倍，很难看出执行分片会有什么需求；

3、目标：提供约 1.3 MB/s 的数据可用性层和完整的分片功能（目前最大数据容量的 10 倍，平常容量的 200 倍）；

4、自 2019 年底以来，数据分片一直是以太坊的目标；

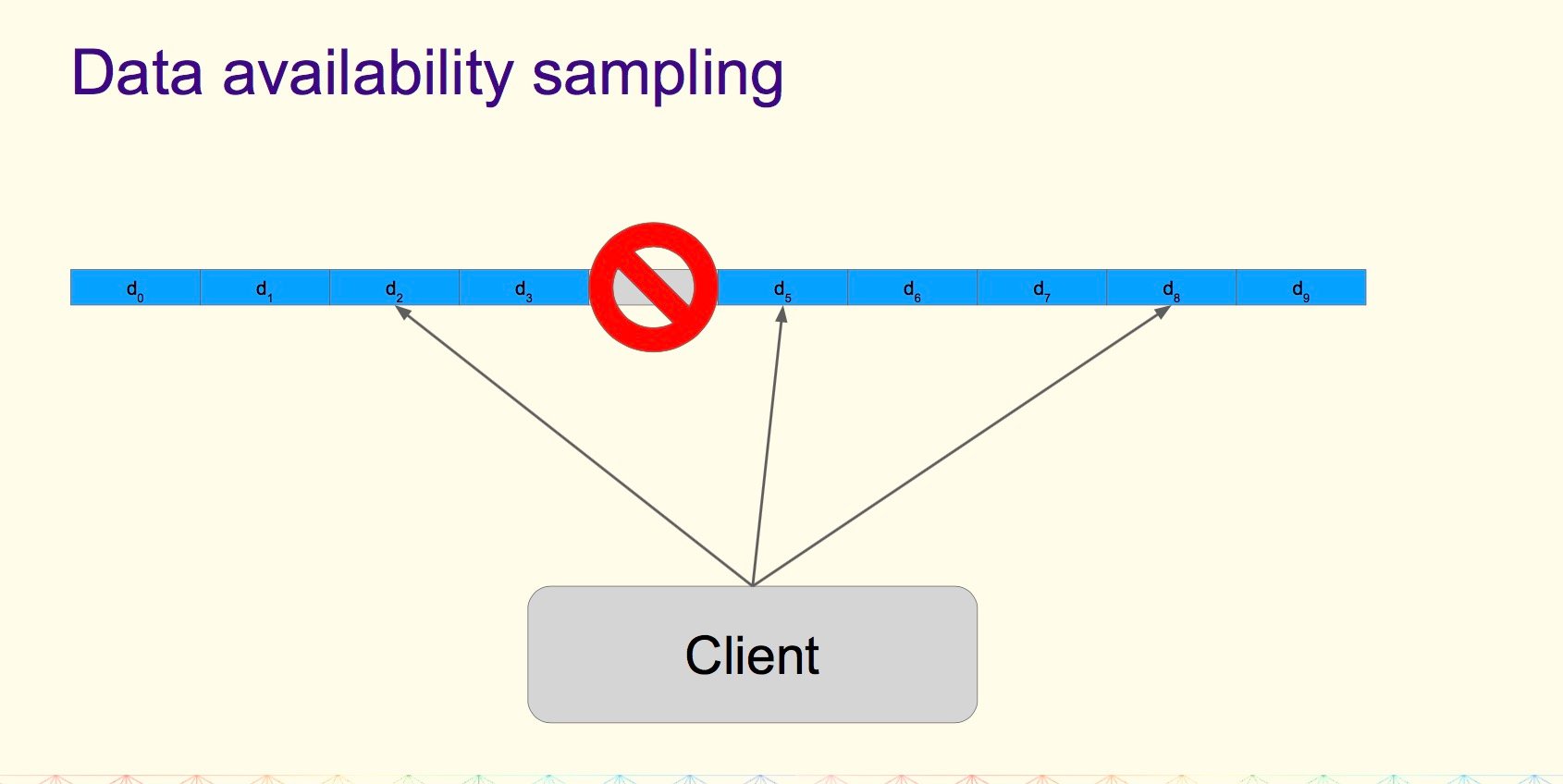
1.2 数据可用性采样（DA sampling）

1、想知道通过 O(1) 工作获得的 O(n) 数据是可用的；

2、思路：将数据分布到 n 个 chunk 分块中；

3、每个节点下载 k 个（随机选择的）chunk 分块；

1.3 纠删码（Erasure coding）

1、使用 Reed-Solomon 编码（多项式插值）扩展数据；

2、例如，在编码率 r=0.5 时，这意味着任何 50% 的区块（d0 到 e4）都足以重建整个数据；

3、现在采样变得高效（例如，查询 30 个随机区块，如果全部可用，超过 50% 不可用的概率为 2 ^ (-30)）

4、但是，我们需要确保编码是正确的；

1.4 KZG 承诺（KZG Commitments）

1、多项式

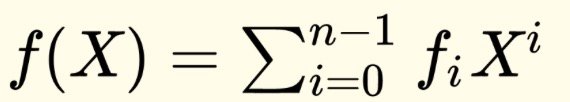
2、承诺 C(f)

3、评估 y = f(z)

（1）证明者可以计算证明 （f,z）

（2）使用 C(f),（f,z）， y 以及 z，验证者可以确认 f(z) = y

4、C(f) 以及 （f,z） 是一个椭圆曲线元素（每个 48 字节）

1.5 KZG 承诺作为数据可用性根

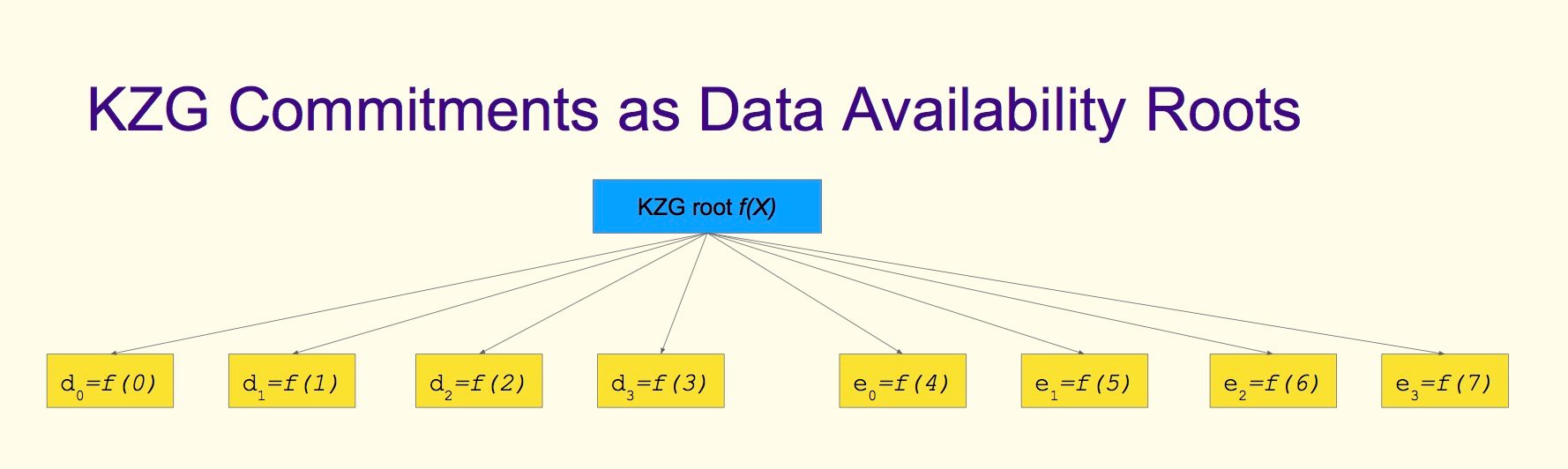
1、将「KZG 根」想象成类似于 Merkle 根的东西；

2、不同之处在于「KZG 根」承诺了一个「多项式」（所有点都保证在同一个多项式上，而 Merkle 根不能保证这一点）；

1.6 分离分片提案

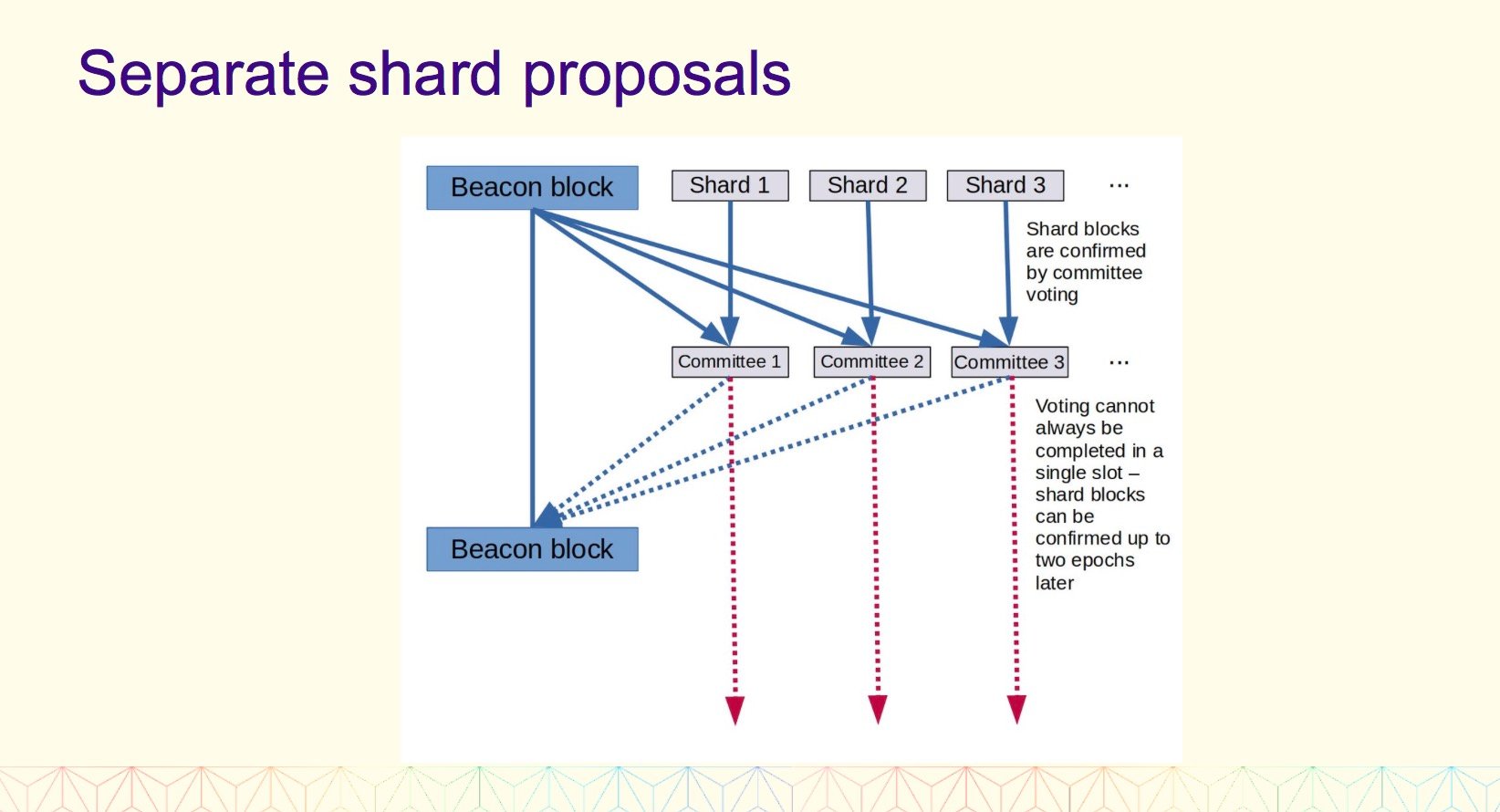
二、 什么是新的

2.1 提议者-构建者（数据生成者）分离 (PBS)

1、被发明用来对抗 MEV 导致的中心化趋势；

2、MEV 意味着更成熟的参与者可以比普通验证者提取更多的价值，这对大型矿池而言意味着优势；

3、PBS 在一个独立的角色中「包含」了这种复杂性/中心化，并具有诚实的少数假设；

（1）提议者（Proposer）= 验证者，诚实的多数假设意味着高度的去中心化要求；

（2）数据生成者（Builder）= 单独的角色，诚实的少数假设，意味着去中心化只需要确保一个诚实（非审查）的数据生成者；

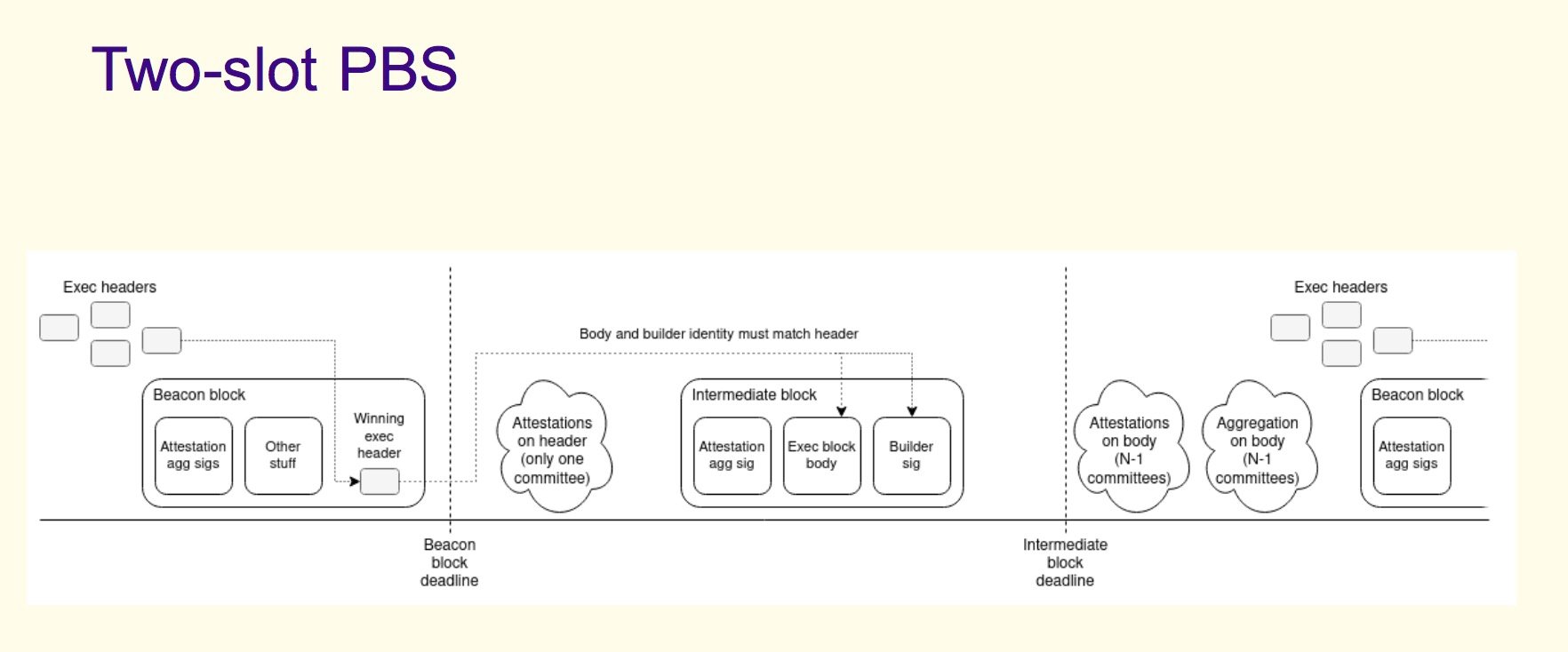
2.2 审查阻力方案 – crList

1、PBS 的危险之处：一个高效的构建者（Builder）可以（以一定的经济成本）永久审查一些交易；

2、[注：在今天的贿赂模型中， 审查一笔交易的成本是永久贿赂所有提议人而不将这笔交易纳入的成本；]

3、crLists 允许提议者指定构建者必须包含的 tx 列表，从而恢复旧的平衡；

crList（「混合 PBS」设计）

2.3 KZG 2d 方案

1、为什么不在 KZG 承诺中编码所有内容？

（1）需要一个超级节点（「构建者」）来构建和重建以防失败的情况；

（2）我们希望避免这种假设的有效性；

2、目标：在 d 个 KZG 承诺中编码 m 个分片 blob；

（1）如果我们天真地去这样做，那就需要 m * k 个样本，这样数据就太多了；

（2）相反，我们可以再次使用 Reed-Solomon 编码将 m 个承诺扩展到 2* m 个承诺；

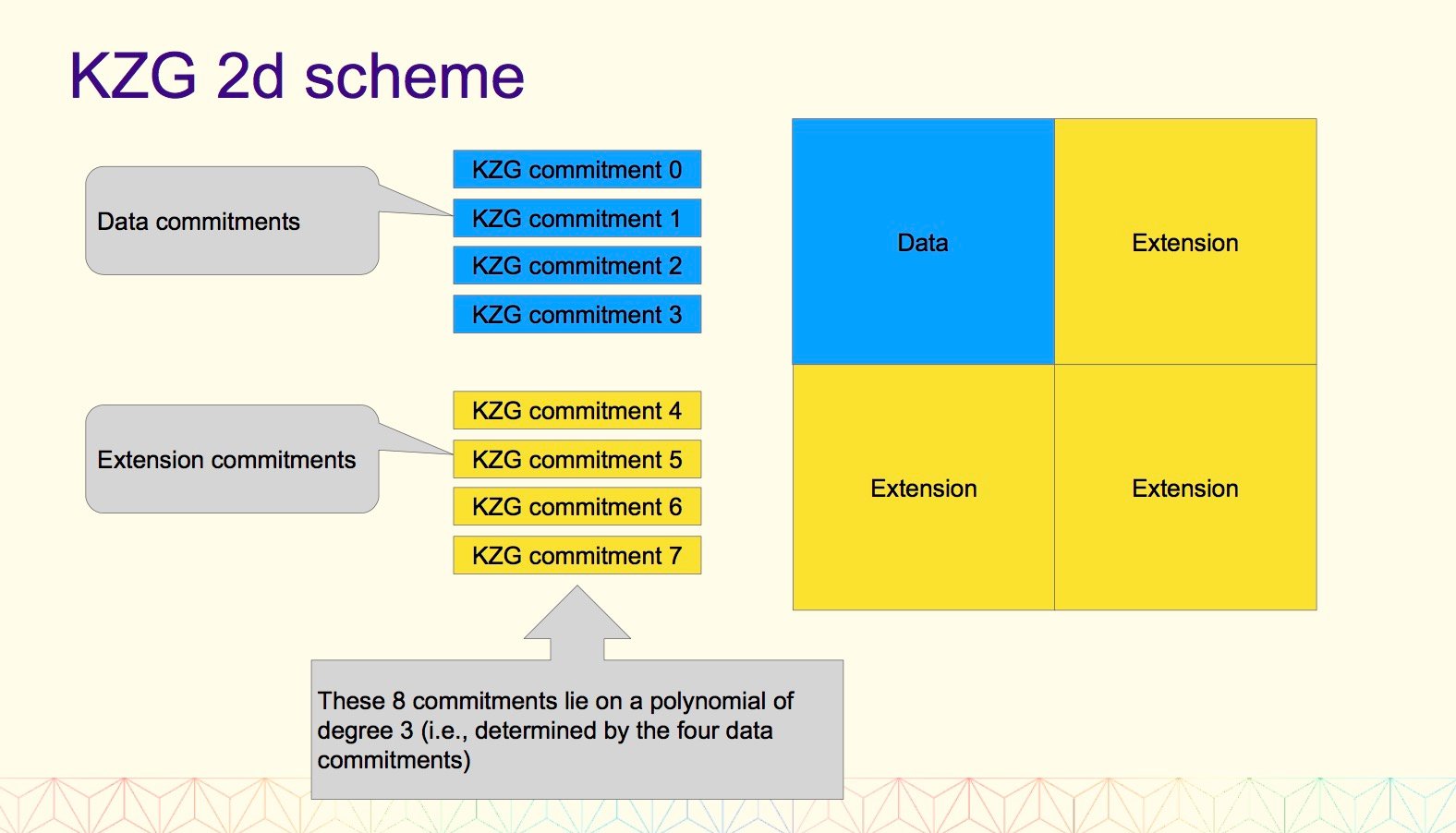
2.4 KZG 2d 方案属性

1、所有样本都可以直接根据承诺进行验证（没有欺诈证明！）；

2、恒定数量的样本确保概率数据可用性；

3、如果 75%+1 的样本可用：

（1）所有数据都可用；

（2）它可以从只观察行和列的验证器中重构；

（3）不需要节点观察所有的情况；

三、组合在一起就是 Danksharding

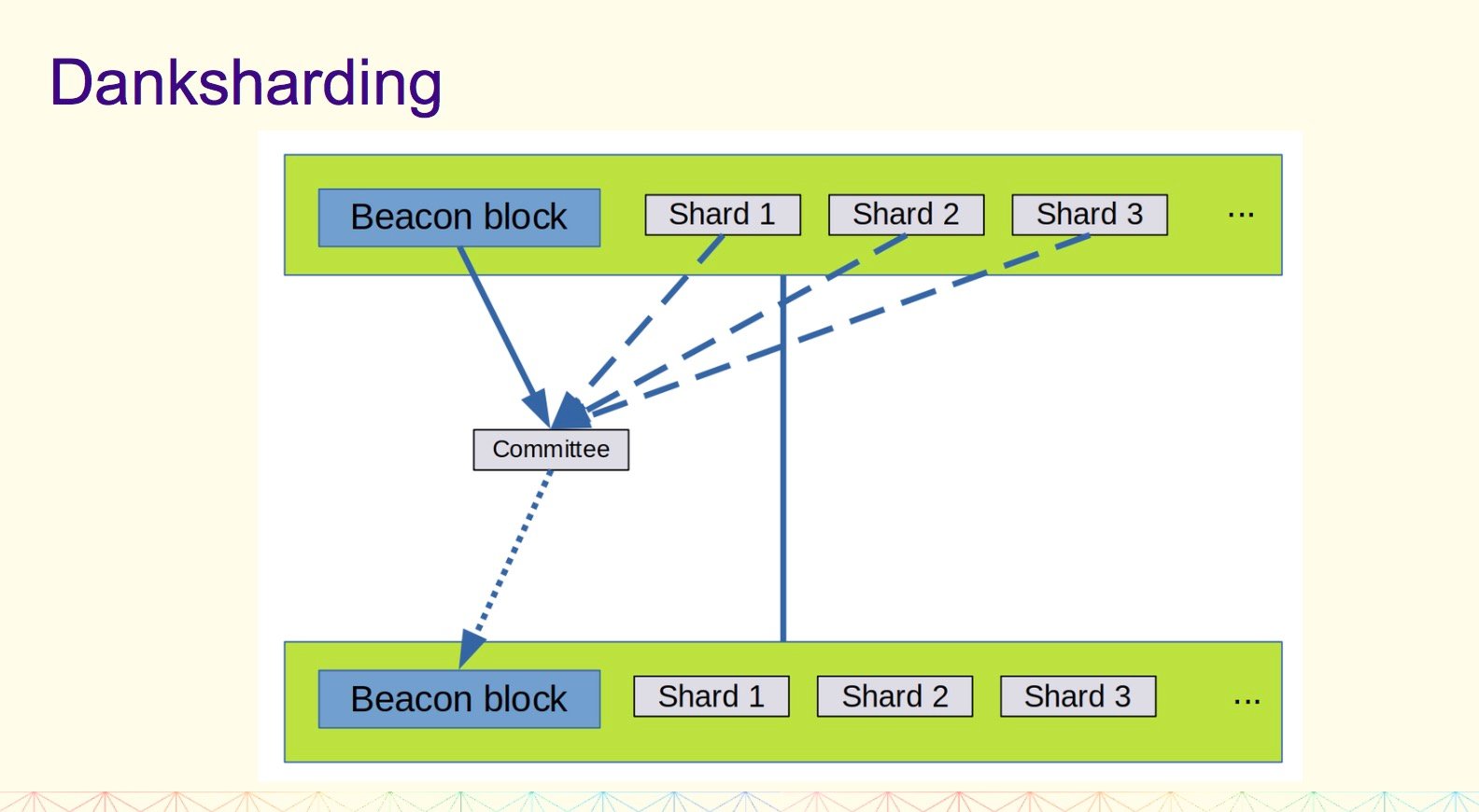
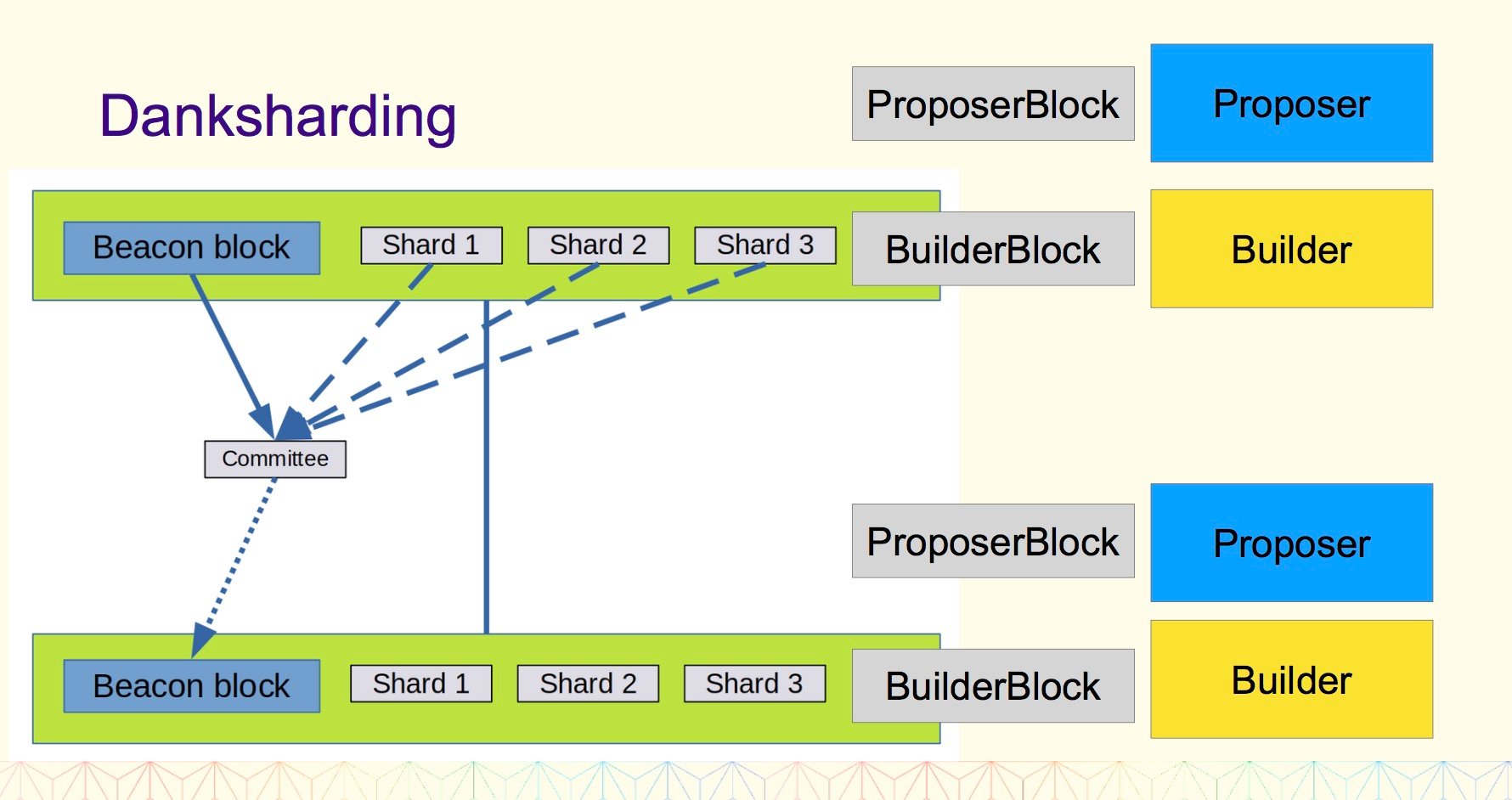
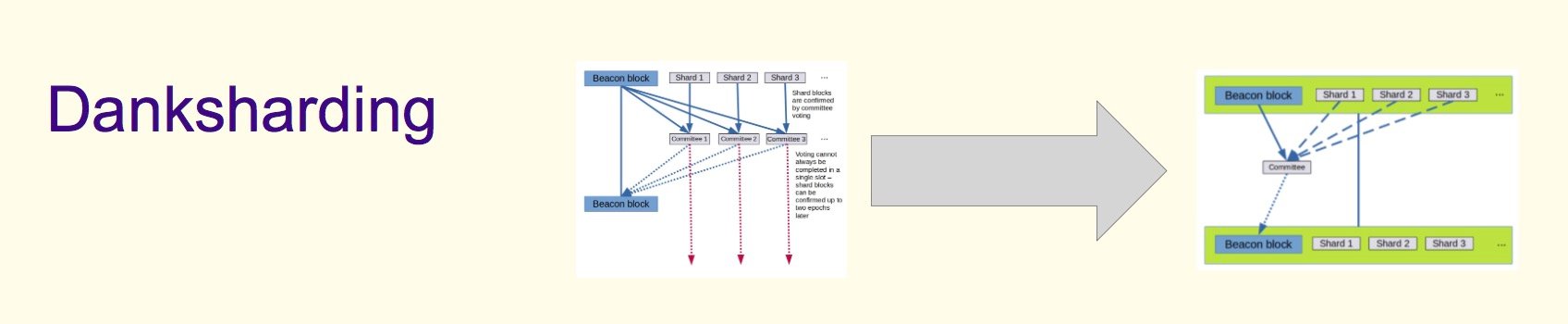
1、执行区块和分片区块是一起构建的；

（1）我们以前需要分片委员会，因为每个分片 blob 可能无法单独使用；

（2）现在，数据生成者的责任是使执行区块有效，并且所有分片 blob 都可用；

2、 验证可以是聚合的；

3.1 Danksharding 诚实多数验证

1、每个验证者选择 s = 2 随机行和列；

2、仅证明分配的行/列是否可用于整个 epoch 时期；

3、一个不可用的区块（<75% 可用）不能获得超过 2^(-2s) = 1/16 的证明；

3.2 Danksharding 重构

1、每个验证者都应该重构他们遇到的任何不完整的行/列；

2、这样做时，他们应该将丢失的样本转移到正交线；

3、每个验证器可以在行/列之间传输 4 个缺失的样本（大约 55,000 个在线验证器可保证完全重构）

3.3 Danksharding DA 采样（恶意多数安全）

1、未来升级

2、每个全节点检查方块矩阵上的 75 个随机样本；

3、这确保了不可用区块通过的概率< 2 ^(-30);

4、带宽 75*512 B / 16s = 2.5 kb/s；

四、总结优点和缺点

优点：

1、简单的设计：

（1）不需要分片委员会基础设施；

（2）不需要跟踪分片 blob 确认；

（3）没有额外的构建者基础设施（来自执行层的同步支付取代了这一点）

（4）可以使用现有的执行层费用市场基础设施；

2、执行链和分片之间的紧密耦合：

（1）使得 rollup 设计更简单；

（2）zkRollup 和执行链之间的同步调用是可能的；

3、分片不需要单独的 PBS；

4、随着数据立即被验证者集的 1/32（而不是旧分片方案中的 1/2048）确认，并在一个 epoch 时期内增加到完整的验证者集，抗贿赂的能力增强了；

5、得益于 2d 方案，全节点（无需运行验证器）将能通过 75 个样本（2.5 kb/s）确保数据可用性，而不是 30*64=1920 个样本（60 kb/s）；

新的挑战：

1、增加了数据生成者要求：

（1）构建 32MB 数据的 KZG 证明（需要 100 核，但目前正在研究 CPU 实现）

（2）需要 2.5 GBit/s 的互联网连接来分发样本；

2、为数据生成者提供了更多权力，因为他们充当了执行+数据层服务提供商；

（1）需要通过 crList 缓解；

相关资源

Danksharding:

Summary doc: https://notes.ethereum.org/@dankrad/new_sharding

Consensus PR: https://github.com/ethereum/consensus-specs/pull/2792

KZG 承诺介绍：

https://docs.google.com/presentation/d/1hEGJd1pT5NpuiHlw91ys6jFpDbNA2ahq5oRWkEk9BRQ

Two-slot PBS: https://ethresear.ch/t/two-slot-proposer-builder-separation/10980

crList 总结：https://notes.ethereum.org/@fradamt/H1ZqdtrBF

原文链接

欢迎加入律动 BlockBeats 官方社群：

Telegram 订阅群：https://t.me/theblockbeats

Telegram 交流群：https://t.me/BlockBeats_App

Twitter 官方账号：https://twitter.com/BlockBeatsAsia