如何设计出一种精妙绝伦的证明递归方案

Fox Tech

23-02-24 22:00

阅读本文需 13 分钟

AI 总结

看总结

原文标题：《如何设计出一种精妙绝伦的证明递归方案》

原文作者：林彦熹，Fox Tech CTO；孟铉济，Fox Tech 首席科学家

前言：在 zkRollup 以及 zkEVM 赛道所遇到的几乎所有难题，其本质都是算法问题。ZKP 硬件加速之所以屡屡被提及，主要原因是当下算法普遍较慢。为了避免落入“算法不够，硬件来凑”的尴尬境地，我们应该从本质算法上解决问题。设计出一种精妙绝伦的递证明方案是解决这个问题的关键。

随着智能合约的不断发展，越来越多的 web3 应用逐步问世，以太坊等传统 Layer1 交易量迅速攀升并随时可能发生拥堵。如何在保证能获取 Layer1 提供的安全性的同时获得更高的效率成为了亟需解决的问题。

对于以太坊而言，zkRollup 使用零知识证明算法作为底层构件，将原本需要在 Layer1 上执行的高昂的计算搬到链下，并向链上提供执行正确性的证明。该赛道主要有 StarkWare、zkSync、Scroll 以及 Fox Tech 等项目。

事实上，在 zkRollup 的设计中，对于效率有很着高的要求：希望提交的证明值足够的小，这样可以减轻 Layer1 的计算量。而为了获取足够小的证明长度，各个 zkRollup 项目都在改进算法以及架构设计，例如 Fox 就结合了最新的零知识证明算法开发了自己的证明算法 FOAKS，来获得最优的证明时间和证明长度。

此外，在验证证明的阶段，最平凡的手段是线性的生成证明并依次验证。为了提高效率，大家首先想到的是多个证明打包成一个证明，这也就是通常提到的证明聚合（Proof Aggregation）。

直观来讲，对于 zkEVM 生成的证明进行验证是一个线性的过程，验证者（Verifier）需要依次验证每一个生成的证明值。但是这种验证方式的效率比较低，通讯开销也比较大，对于 zkRollup 的场景，更高的验证者端的开销就意味着更多的 Layer1 层的计算，也就会导致更高的 Gas fee。

我们先看一个例子：Alice 想要向全世界证明自己在本月的 1 号至 7 号都去了 Fox 公园。为此，她可以分别在 1 号至 7 号的每一天都拿着当天的报纸在公园拍一张照片，这 7 张照片打包就成为一个证明。

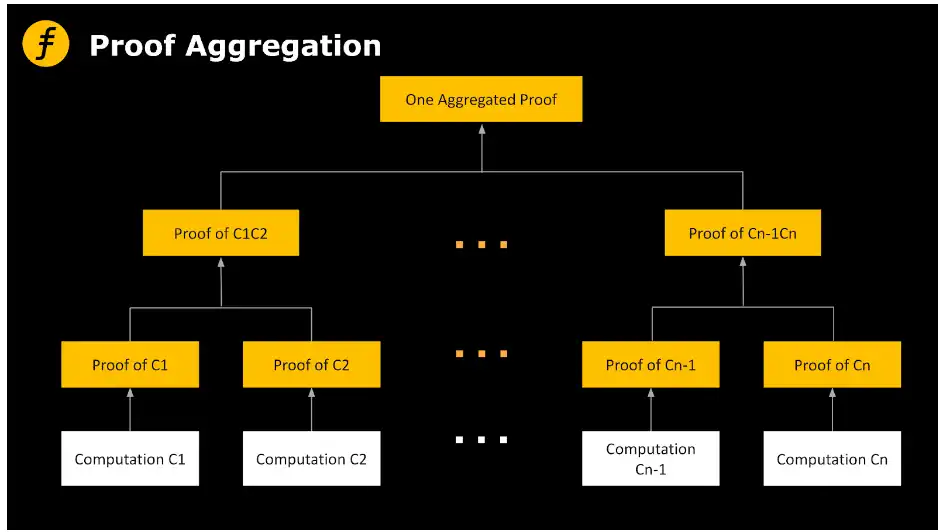
图 1：一般意义的证明聚合方案

上面例子里把 7 张照片直接放入一个信封就是直观意义上的证明聚合，这在实际情况中对应的是将不同证明连接在一起并依次线性验证，即先验证第一个证明，再验证第二个证明以及随后的证明。问题是这种做法既不会改变证明的大小，也不会改变证明的时间，与一个一个去证明并验证的效果一样。如果要实现对数级别的空间压缩，那就要使用下面提到的递归证明（Proof Recursion）。

Halo2 以及 STARK 所用证明递归方案

为了更好的说明什么是递归证明，我们回到上面的例子。

Alice 的 7 张照片实际上是 7 个证明。现在考虑将它们合并起来，于是 Alice 可以在 1 号拍好照片，在 2 号拿着这张照片和 2 号的报纸拍照片，在 3 号再拿着 2 号拍的照片和 3 号的报纸拍照片。以此类推，Alice 在 7 号拿着 6 号的照片和 7 号的报纸拍下最后一张照片，而其他小伙伴在看到 7 号的这最后一张照片，就可以验证在 1～7 号 Alice 都去了公园。可以看到，之前的七张证明照片，被压缩成了一张。而在这个过程中的一个关键技巧，即是“包含照片的照片”，相当于将之前的照片以递归的形式嵌套进了之后的照片当中。这跟把很多照片放一起再拍个照片是不同的。

zkRollup 的递归证明技巧可以大幅压缩证明大小。具体来讲，每一笔交易都会生成一个证明，我们设原始的交易计算电路为 C0，P0 为 C0 的正确性证明，V0 为验证 P0 的计算过程，证明者（Prover）将 V0 也转化为对应的电路，记作 C0’。此时，对于另一笔交易的证明计算过程 C1，就可以将 C0’和 C1 的电路合并，这样一来，一旦验证了合并后的电路的正确性证明 P1，就相当于同时验证了以上两笔交易的正确性，也就是实现了压缩。

而回顾上述过程可以发现，其实压缩的原理在于将验证证明的过程又转化为了电路，然后生成“对于证明的证明”，所以从这个角度来说，是一种可以不断向下递归的操作，因此也被成为递归证明。

图 2：Halo2 与 Stark 所使用的递归证明方案

Halo2 与 STARK 所采用的 Proof Recursion 方案能够并行生成证明，并将多个证明进行合并，使得验证一个证明值的同时可以验证多个交易执行的正确性，那就能够压缩计算的开销，从而极大的提高系统的效率。

然而，这样的优化仍然停留在具体的零知识证明算法之上的层次，为了进一步提高效率，我们需要更底层的优化和创新，Fox 设计的 FOAKS 算法通过将递归的思想应用在一个证明的内部做到了这点。

FOAKS 所使用的证明递归方案

在 Fox Tech 是一个 zkEVM-based 的 zkRollup 项目。在它的证明系统中，同样使用递归证明的技巧，但是内涵与上述递归方式有不同之处，主要的区别是 Fox 是在一个证明的内部使用了递归 (Recursion) 的思想。为了表达出 Fox 所使用的递归证明的那种不断将要证明的问题约化，直到约化后的问题足够简单的核心思想，我们需要再举一个例子。

在上面的例子，Alice 通过拍照证明自己在某天去了 Fox 公园，于是 Bob 提出了不同的建议，他认为证明 Alice 去过公园的问题可以被约化为证明 Alice 的手机去过了这个公园，而证明这件事又可以被约化为证明 Alice 手机的定位在公园的范围里。因此，为了证明 Alice 去过这个公园，她只要在公园的时候用她的手机发送一个定位就行了。如此一来证明的大小就从原本的一张相片 (一个很高维的数据) 变为一个 3 维的数据 (经纬度和时间)，有效的节约了成本。这个例子并不完全恰当，因为也许有人会质疑 Alice 的手机到过 Fox 公园不代表 Alice 本人到过，但是在实际的情况中，这个约化过程是数学形式上严格的。

具体而言，Fox 的递归证明的用法是在电路层面的递归。在进行零知识证明的时候，我们会将要证明的问题编写成电路，接着通过电路计算出一些需要满足的等式。而与其展示这些等式是满足的，我们再次将这些等式编写成电路，如此往复，直到最后要证明满足的等式变得足够简单，我们便能轻松的直接证明了。

从这个过程当中我们可以看出，这么做更贴近“递归”的含义。值得一提的是不是所有算法都可以使用这个递归技术，假设每一次递归会将复杂度为 O(n) 的证明变为一个 O(f(n)) 的证明，而这个递归过程本身的计算复杂度是 O(g(n))，则递归一次后总计算复杂度就变为 O1(n)=O(f(n))+O(g(n))，两次后就是 O2(n)=O(f(f(n)))+O(g(n))+O(g(f(n)))，三次后就是 O3(n)=O(f(f(f(n))))+O(g(n))+O(g(f(n)))+O(g(f(f(n))))，...，以此类推。因此，只有在 f 和 g 两个对应算法特性的函数满足对某个 k 有 Ok(n)<O(n) 时，这样的递归技术才能有效发挥作用。在 Fox 当中便有效的使用了这个递归技术压缩证明复杂度。

图 3：ZK-FOAKS 所使用的递归证明方案

结语

证明的复杂度一向是零知识证明应用中最重要的关键之一，证明复杂度这个性质随待证明的事情越来越复杂会变得越来越重要，特别是在像 zkEVM 这样的巨型 ZK 应用场景中，证明的复杂度会对产品的性能与用户的体验造成决定性的影响。而在众多降低最终证明的复杂度的方法中，对核心算法的优化最为重要，Fox 在最前沿算法的基础上设计出了精妙绝伦的递证明方案，并利用这项技术打造出最适合于 zkEVM 的 ZK-FOAKS 算法，有望成为 zkRollup 界的性能担当。